English
Zadanie Ciągi de Bruijna drugiego rodzaju (deb)
Type Two de Bruijn Sequences
Memory limit: 32 MB
A word 
composed of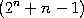 
characters 0 and 1
is called a de Bruijn sequence of order 
if
every 
-character word composed
of zeroes and ones is its subword - that is a fragment of consecutive
characters - of 
.
An example of a de Bruijn sequence of order 3 is 0001011100.
A type two de Bruijn sequence of order 
is such a word 
of arbitrary length that each 
-character word composed of zeroes
and ones is a subsequence - that is a fragment of not necessarily
consecutive characters - of 
.
An example of a type two de Bruijn sequence of order 3 is
00101101.
As far as we know, Nicolaas Govert de Bruijn did not invent such sequences,
but their definition is similar to the previous one, isn't it?
Let us consider a word 
composed only of zeroes and ones.
How many digits (0 or 1, of course) have to be added
at the end of 
for the word to become a type two de Bruijn sequence
of order 
?
Input
The first line of the standard input contains two integers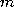 
and 
(
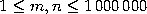), separated by a single space.
The second line contains an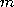 
-character word 
composed only of
digits 0 and 1 that does not contain any spaces.
Output
The first and only line of the standard output should contain
a single non-negative integer, denoting the minimal number of digits
that need to be added at the end of the word 
for it to become
a t.t.d.B.s. of order 
.
Example
For the input data:
5 3 00101
the correct result is:
2
Explanation of the example: After adding the characters 01
we obtain the following t.t.d.B.s. of order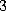 
: 0010101.
Task authors: Marek Cygan and Jakub Radoszewski.